| Artikelen | deel: |
verrijkingsleerstof
Voorwaarden tot differentiatie
INLEIDING
Binnen de klassen differentiëren is een noodzaak om onderwijs op maat te garanderen voor iedereen, zowel naar boven (begaafde leerleerlingen) als wel naar beneden (zorgleerlingen) moet de leerkracht in de klas in staat zijn om te differentiëren .
Bij de uitvoering van dit streefdoel schort er vaak heel wat aan, niet alleen door gebrek aan organisatie of pedagogische ondersteuning door begeleidende instanties, maar vooral vanwege het ontbreken van voldoende en aangepast differentiatiemateriaal.
Het vergt van de leerkracht zeer veel, op gebied van klassenorganisatie, didactische vaardigheden, administratie, samenwerking met andere instanties en ouders. Om aan de vragen en behoeften van (hoog)begaafde leerlingen te kunnen voldoen, ontbreekt het de leerkracht vaak nog aan aangepast verbredings-en verdiepingsmateriaal. Vooral voor wiskunde is het belangrijk dat knappe rekenaars ook op hun vermogen worden aangesproken. Binnen de Vrije School ontbreekt het materiaal ter differentiatie vooral tijdens de oefenuren en oefenmomenten binnen het hoofdonderwijs.
Om te kunnen komen tot verdieping, verbreding ofwel om te differentiëren zijn er een aantal basisvoorwaarden van belang.
BASISVOORWAARDEN
De begaafde kinderen, die we in staat willen stellen hun vermogens en vaardigheden te verdiepen, moeten in staat zijn met een minimale uitleg aan de slag te gaan en zonder hulp of aansporing verder te werken (intrinsieke motivatie). De belasting voor de leerkracht moet minimaal zijn.
Differentiatie op dit gebied mag niet leiden tot extra correctiewerk voor de leerkracht. In de wijze van aanpak (materiaal dat ter verdieping wordt aangeboden) dient een systeem van zelfcorrectie door de leerling ingebouwd te zijn.
De verbredingsleerstof dient een systematische opbouw te hebben. Het verbredingsprogramma moet logisch opgebouwd zijn en een innerlijke consistentie bevatten. Losse blaadjes zonder verleden ( = geen verband met vroegere leerstof) of toekomst (een vervolg ontbreekt) kunnen een tijdelijke oplossing bieden maar helpen een kind niet om zijn vermogens en vaardigheden uit te bouwen.
4. Voldoende tijdsinvestering door de leerling![]()
De verbredingstaken moeten voldoende uitdaging bezitten en van de leerling een echte inspanning vergen. Aan ieder blad of pakketje moet minstens een half uur gewerkt kunnen worden om te vermijden dat de klas door voortdurend heen en weer geloop wordt gestoord.
Differentiatie op dit gebied is geen stuntwerk dat van uur tot uur, van dag tot dag of van jaar tot jaar de leerprocessen bijstuurt. Aanpak van (hoog)begaafde leerlingen veronderstelt een visie op lange termijn. De systematische opbouw van verbredingsleerstof moet zich uitstrekken over de ganse schoolperiode van het kind. Verbredingsleerstof is dus geen kunst- en vliegwerk van het moment of het initiatief van een individuele leerkracht die zich met veel goede wil ontfermt over een kind. Een school met een goed doordachte visie op dit vlak zal dit ook vermelden in het schoolwerkplan.
6. Behoorlijk niveau van technisch en begrijpend lezen![]()
Opdat leerlingen zelfstandig zouden kunnen werken aan het verbredingsprogramma is een behoorlijk leesniveau noodzakelijk. Vooral in het eerste leerjaar kan dit wel eens problemen geven.
Een voorbeeld van bruikbaar materiaal binnen de Vrijeschool is Somplex. Hieronder vind je een overzicht van de inhoud van deze verdiepingsmethode.
Echter ook Plustaak van de methode Pluspunt levert een schat aan materiaal.
Daarnaast valt ook te denken aan allerlei raadsels, die inzicht van leerlingen vragen.
Somplex
De vijf categorieën met inhoud zijn:
Categorie |
Inhoud |
1. Strategieën |
Handigheid, redeneren, proberen, magische figuren, combinatoriek (mogelijke volgorde, combinaties en dergelijke).Diagram (kolom, staaf, sector, beeld) grafiek (beeld, lijn), tabellen, kansberekening, gemiddelde. |
2. Figuren |
Patronen, symmetrie, spiegelen, diverse invalshoeken, kubus, driehoek, vierkant, cirkel, pijltjesopdrachten, coördinaten. |
3. Maten |
Lengte, omtrek, oppervlakte, gewicht, inhoud, tijd, geld, temperatuur, schaal, vergroten, verkleinen, verhoudingen. |
4. Getallen |
Tellen, verzamelen, ordenen, vergelijken, structuren, splitsen, afronden, (on)even getallen, priem-, driehoeks-, en vierkantsgetallen, plaatswaarde. |
5. Bewerkingen |
Plus, min, maal, delen, deelbaarheid, ontbinden in factoren, machten, breuken, decimale getallen, tekens als &, reeksen, procenten. |
Om het werken met de verrijkingsleerstof ordentelijk te laten verlopen, moet de leerkracht een keuze maken uit verschillende mogelijkheden:
- Eerste versnelling: de leerling moet eerst de totale basisstof doorwerken in eigen tempo vooraleer hij met verrijkingsstof kan starten.
- Tweede versnelling: de leerling mag de ingekorte basisstof doorwerken in eigen tempo en daarna direct overschakelen naar de verrijkingsleerstof.
De aldus ingewonnen tijd kan op verschillende manieren gevaloriseerd worden:
- Per les: nadat de leerlingen de oefeningen van de les hebben afgewerkt, krijgen zij de toelating om met Somplex te werken.
- Per week: zodra de leerling het weekprogramma voor rekenen heeft afgewerkt, mag hij met Somplex werken.
- Per blok: zodra de leerling een leerstofblok heeft afgewerkt mag hij op Somplex overschakelen.
Werkwijze 2 of 3 verdienen de voorkeur. Zowel qua klasorganisatie, volging door de leerkracht, correctie en feedback is het beter om versplintering tegen te gaan en in grotere blokken te werken.

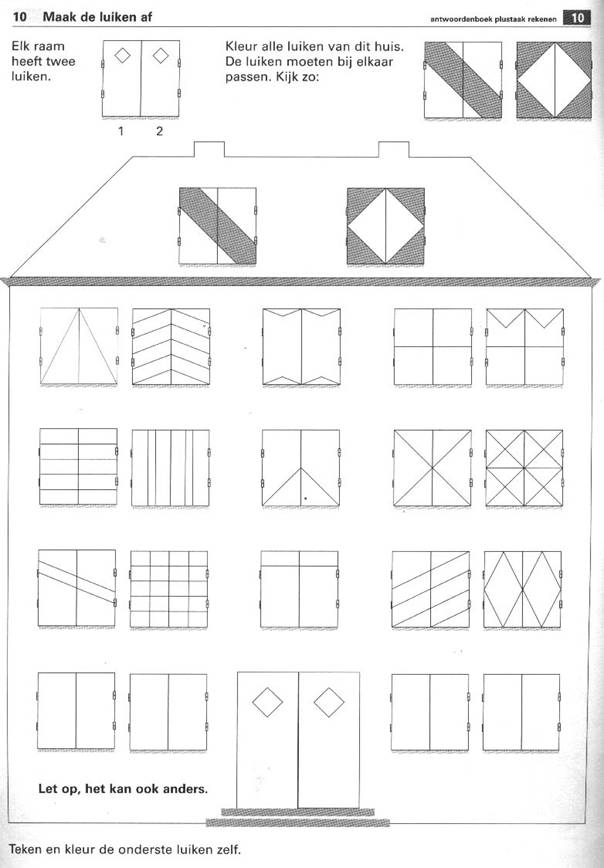
Plustaakvoorbeelden 
Somplexvoorbeelden
Raadsels 
De inhoud van het vogende stuk is overgenomen uit de rekenkranten.
Opmaak is veranderd. U ziet alleen de opdrachten
![]()
- Zet alle getallen van 1 tot 11 in de verschillende vakken zodat de som van de cijfers zowel horizontaal als vertikaal steeds 20 is.
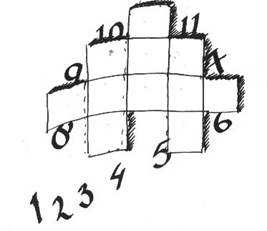
- In de zeven rondjes van deze puzzel moeten de volgende getallen ingevuld worden: 12, 20, 24, 32, 44, 48 en 56 Als ze goed worden ingevuld is de som van de aangegeven richting 100.
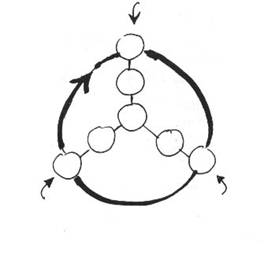
- Ik ben benieuwd of iemand van deze opgave de antwoorden kan vinden
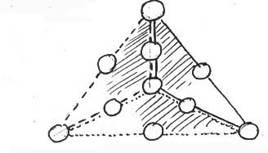
In deze driehoek worden de getallen van 1 t/m 10 zo verdeeld dat alle driehoeken (zie voorbeeld) het zelfde antwoord kennen. Bij voorbeeld De som is: 29 De som van: 8,9,6,2,1,3=29
De som van: 8,7,5,2,4,3=29
De som van: 6,1,3,4,5,10=29
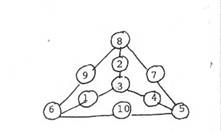
Doe dat ook met de volgende uitkomsten
De som is: 30
De som is: 31
De som is: 32
De som is: 33
De som is: 34
De som is: 35
De som is: 36
De som is: 37